
Problem 🔒
문제
https://www.acmicpc.net/problem/1967
트리(tree)는 사이클이 없는 무방향 그래프이다. 트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다. 트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다. 이럴 때 트리의 모든 노드들은 이 두 노드를 지름의 끝 점으로 하는 원 안에 들어가게 된다.
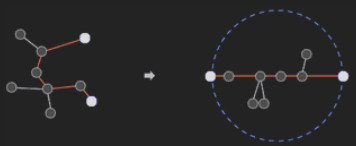
이런 두 노드 사이의 경로의 길이를 트리의 지름이라고 한다. 정확히 정의하자면 트리에 존재하는 모든 경로들 중에서 가장 긴 것의 길이를 말한다.
입력으로 루트가 있는 트리를 가중치가 있는 간선들로 줄 때, 트리의 지름을 구해서 출력하는 프로그램을 작성하시오. 아래와 같은 트리가 주어진다면 트리의 지름은 45가 된다.
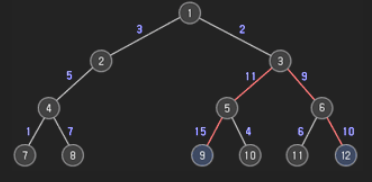
트리의 노드는 1부터 n까지 번호가 매겨져 있다.
입력
파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호를 나타내고, 두 번째 정수는 자식 노드를, 세 번째 정수는 간선의 가중치를 나타낸다. 간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.
출력
첫째 줄에 트리의 지름을 출력한다.
예제 입력 1
12
1 2 3
1 3 2
2 4 5
3 5 11
3 6 9
4 7 1
4 8 7
5 9 15
5 10 4
6 11 6
6 12 10
예제 출력 1
45
트리의 조건 🌲
- 트리는 모든 노드가 하나의 연결된 그래프를 이루어야 한다.
- 트리는 계층형 자료구조이기 때문에, 사이클이 없는 그래프이다.
- 사이클(Cycle) : 그래프에서 노드가 자신에게 다시 도달할 수 있는 경로를 말한다.
- 예를 들어, 노드A → 노드B → 노드C → 노드A 와 같은 형태를 말한다.
- 트리는 두 노드 간에 반드시 하나의 유일한 경로만 존재한다.
Approach ⭕
- 트리의 지름 찾는 방법
- 트리의 지름은 트리에서 가장 먼 두 노드 사이의 거리를 말한다.
- 첫번째로, 임의의 노드에서 가장 먼 노드(노드 A)를 찾는다.
- 이 때 찾은 노드 A가 트리의 지름에서 한쪽 끝점에 해당한다.
- 두번째로, 노드 A에서 가장 먼 노드(노드 B)를 찾는다.
- 노드 A에서 가장 먼 노드 B가 트리 지름의 다른 끝점에 해당한다.
- 트리는 사이클이 없고, 두 노드 간에 유일한 경로가 존재하기 때문에, 항상 이 방법이 옳다고 할 수 있다.
- 간선 정보 입력
- 1번부터 N번 노드까지 간선을 입력 받는 반복문을 생성한다.
- 간선의 개수를 모르니, while 문으로 반복문을 생성한다.
- 연결된 노드 번호 v가 -1이면 while 문을 탈출한다.
- 간선은 ArrayList에 int 배열에 {노드번호, 가중치} 형태로 저장한다.
- 첫번째 DFS (트리의 지름 한 쪽 끝 점 찾기)
- 임의의 노드(노드 1)에서 시작하여 방문하지 않은 노드를 탐색하며, 경로의 거리를 누적(sum)한다.
- 현재의 누적 거리가 최대 거리(d)보다 크면, 최대 거리(d)를 갱신하고, 노드 번호(node1)를 저장한다.
- 두번째 DFS (트리의 지름 다른 끝 점 찾기)
- 첫번째 DFS로 찾은 트리의 지름 한 쪽 끝 점인 node1에서 다시 탐색하여, 가장 먼 노드까지의 거리를 구한다.
Solution 💡
Idea1. 리프노드에서 리프노드까지 가기
첫번째 아이디어로 트리의 지름 양 끝 점들은 무조건 리프노드 일 것이라 생각했다.
그래서 리프노드에서 리프노드까지의 거리 중 가장 긴 거리를 측정했다.
이 방법은 실패했다. 이유는 트리의 지름 끝 점이 리프노드가 아닌 경우도 있어서였다. ㅠㅠ..
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class 트리의지름 {
static int N, u, v, d, ans=0;
static boolean[] visit, child; // child:자식이 있으면(true)
static ArrayList<ArrayList<int[]>> list = new ArrayList<>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
visit = new boolean[N+1];
child = new boolean[N+1];
for(int i=0; i<N+1; i++){list.add(new ArrayList<>());}
for(int i=0; i<N-1; i++){
u = sc.nextInt();
v = sc.nextInt();
d = sc.nextInt();
list.get(u).add(new int[]{v,d});
list.get(v).add(new int[]{u,d});
child[u] = true; // 노드 u는 자식이 있는 노드
}
System.out.println(Arrays.toString(child));
for(int i=1; i<N+1; i++){
if(!child[i]){
DFS(i, 0);
for(int j=0; j<N+1; j++){visit[j]=false;}
}
}
System.out.println(ans);
}
public static void DFS(int node, int sum){
visit[node] = true;
if(!child[node] && sum!=0){
ans = Math.max(ans, sum);
return;
}
for(int[] a : list.get(node)){
int n = a[0]; // 노드 번호
int d = a[1]; // 가중치
if(!visit[n]){
DFS(n, sum+d);
}
}
}
}
Idea2. 모든 경우의 수
두번째 방법은 모든 경우의 수를 완전 탐색하는 방법이다.
모든 노드에서부터 노드까지 거리 중 가장 긴 거리를 탐색하여 트리의 지름을 찾았다.
문제는 정답으로 통과되었지만, 잘못하면 시간초과가 걸릴 정도로 시간이 굉장히 오래 걸렸다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;
public class 트리의지름 {
static int N, u, v, d, ans=0;
static boolean[] visit, child; // child:자식이 있으면(true)
static ArrayList<ArrayList<int[]>> list = new ArrayList<>();
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
visit = new boolean[N+1];
// child = new boolean[N+1];
for(int i=0; i<N+1; i++){list.add(new ArrayList<>());}
for(int i=0; i<N-1; i++){
StringTokenizer st = new StringTokenizer(br.readLine());
u = Integer.parseInt(st.nextToken());
v = Integer.parseInt(st.nextToken());
d = Integer.parseInt(st.nextToken());
list.get(u).add(new int[]{v,d});
list.get(v).add(new int[]{u,d});
// child[u] = true; // 노드 u는 자식이 있는 노드
}
for(int i=1; i<N+1; i++){
DFS(i, 0);
for(int j=0; j<N+1; j++){visit[j]=false;}
}
System.out.println(ans);
}
public static void DFS(int node, int sum){
visit[node] = true;
for(int[] a : list.get(node)){
int n = a[0]; // 노드 번호
int d = a[1]; // 가중치
if(!visit[n]){
DFS(n, sum+d);
}
}
ans = Math.max(ans, sum);
}
}Idea3. 트리의 성질을 활용한 DFS 2번
import java.util.ArrayList;
import java.util.Scanner;
public class 트리의지름 {
static int N, u, v, d, ans=0, node1=0;
static boolean[] visit;
static ArrayList<ArrayList<int[]>> list = new ArrayList<>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
N = sc.nextInt();
visit = new boolean[N+1];
for(int i=0; i<N+1; i++){list.add(new ArrayList<>());}
for(int i=0; i<N-1; i++){
u = sc.nextInt();
v = sc.nextInt();
d = sc.nextInt();
list.get(u).add(new int[]{v,d});
list.get(v).add(new int[]{u,d});
}
DFS(1, 0);
for(int j=0; j<N+1; j++){visit[j]=false;}
DFS(node1, 0);
System.out.println(ans);
}
public static void DFS(int node, int sum){
visit[node] = true;
for(int[] a : list.get(node)){
int n = a[0]; // 노드 번호
int d = a[1]; // 가중치
if(!visit[n]){
DFS(n, sum+d);
}
}
if(ans<sum){ans = sum; node1 = node;}
}
}

트리의 성질을 활용해 풀었던 아이디어가 완전탐색보다 8배는 빨랐다.
자료구조의 이해 차이로 알고리즘 실행 시간이 이렇게 단축될 수 있다는 것에 놀랐다.
이 문제로 인해서, 트리의 성질은 절대 안까먹게 된 것 같다.
그리고 백준 1167번 트리의 지름도 같은 문제이니 복습겸 한 번 더 풀어도 좋을것 같다.
'코딩 테스트(Coding Test) > 백준' 카테고리의 다른 글
| [백준] 1504번 : 특정한 최단 경로 - 자바(Java) (1) | 2024.11.20 |
|---|---|
| [백준] 2260번 : 회장 뽑기 - 자바(Java) (0) | 2024.11.19 |
| [백준] 1167번 : 트리의 지름 - 자바(Java) (0) | 2024.11.16 |
| [백준] 22856번 : 트리 순회 - 자바(Java) (2) | 2024.11.15 |
| [백준] 1240번 : 노드사이의 거리 - 자바(Java) (3) | 2024.11.14 |